Slope Fields

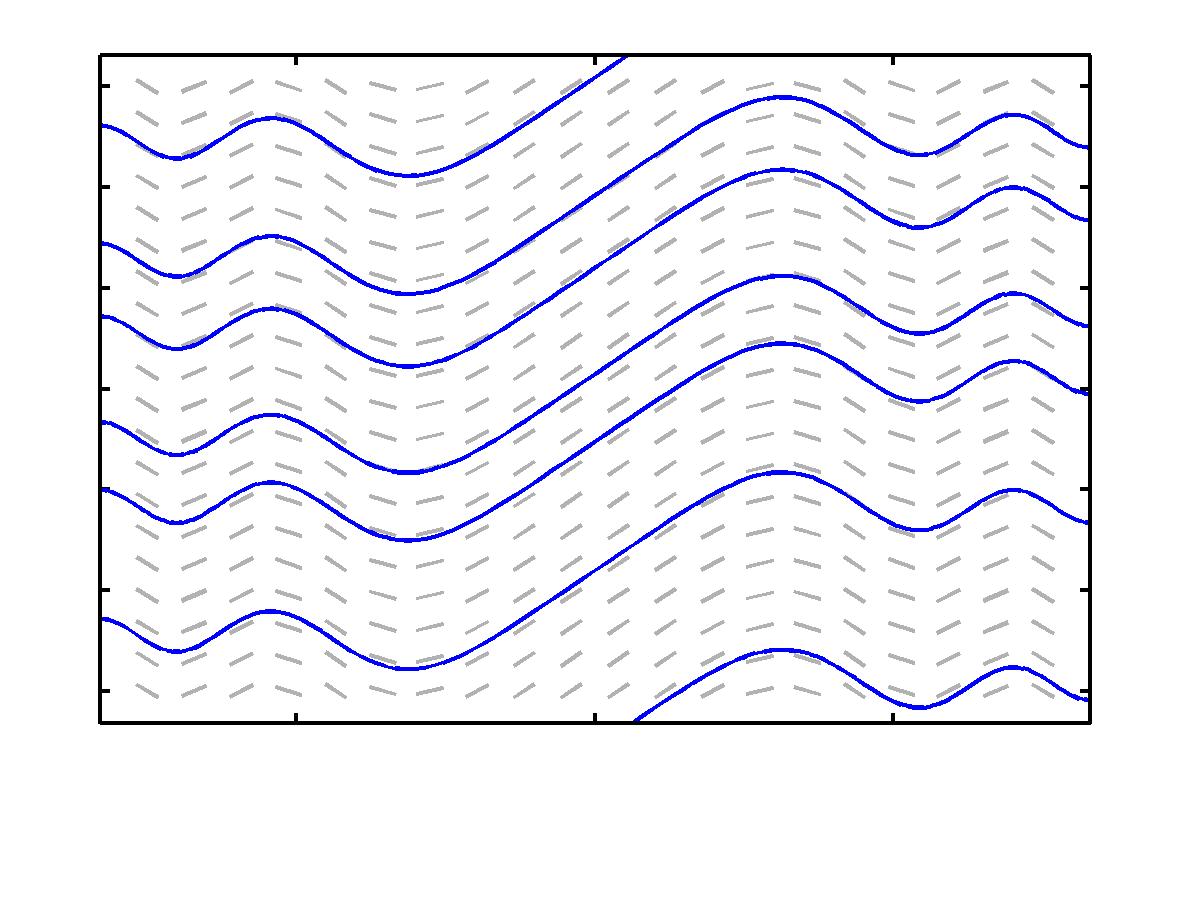
A Slope Field is one type of qualitative tool for studying first order ODEs. In the first order equation,

y' = f(t,y)

the left hand side y' (or dy/dt as we sometimes denote it) represents the rate of change of y with respect to t. If we pick a point (t,y) in the ty-plane, the right hand side f(t,y) gives the value of the rate of change at that point. Note that this assumes that we are analyzing the behavior of a solution to the ODE which actually passes through the given point.

Here is an alternate way of thinking about it. Since y(t) represents the solution curve, then we can also interpret the left hand side of the equation, y'=y'(t) , as the slope of the solution curve at any point on the curve. Again, if we pick a point (t,y) in the ty-plane, the right hand side f(t,y) gives the value of the slope of the tangent to the curve at that point. By choosing a point in the ty-plane and computing the value of fat that point, we are actually computing the slope of the tangent to the solution curve at the point (t,y). We can then use this slope value to draw a small piece of a tangent line at that point. A slope field is nothing more than a graph of lots of mini-tangent lines at various points in the ty-plane. The qualitative behavior of solution curves can then be sketched by following the tangents.

• Click Here for an attractive and helpful (hopefully) online presentation concerning this topic.

Updated on: 08/22/07.